I should probably use this blog more often. Here it sits, gathering dust, while I work on things that people would like to know more about.
A while ago, I started working on a game from Brilliant Skies, Ltd. called From the Depths. Placing the game in a particular genre is difficult: It’s got voxel-building, like Minecraft. It has real-time Strategy elements, like Starcraft. It’s got boats, like… Well, I can’t think of a game with boats. Harpoon, maybe? Whatever the case may be, it’s a naval combat simulator with building elements, and is great fun to play and work on.
One of my projects in From the Depths is working on the Lua API for ships. I’ve added some new features to it about six months ago, and while well-received, it was made to work with my hacky pre-hire method of injecting it into the game as a mod, rather than smoothly integrating it with all the other API elements. I finally have time to work on it again, and I’ve made some major changes to it. One of them is to move all the missile stuff to its own classes, and add in a delay system for commands sent to missiles, as a function of distance. The reason for this is to permit us to bring down Lua missiles a notch, since they are considered by Nick and I – not to mention our users – as a tad overpowered.
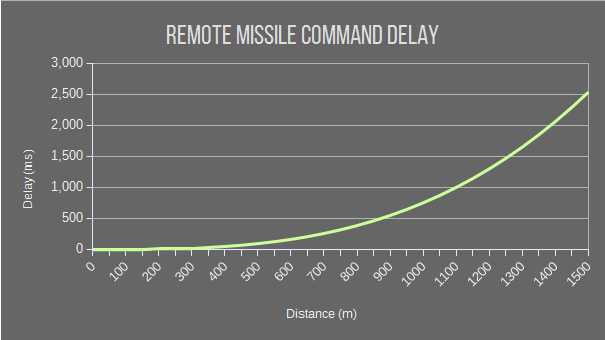
Basically, when you send a command to a missile (such as setting the AimPoint or a register), the delay is added to the missile’s Lua Transceiver block. The transceiver sends messages at a fixed rate, currently 20 messages per second. These messages then take some time to reach the missile (meaning a missile 1km away gets a message 751ms later). If the message queue is full, the command cannot be sent (and there are new properties on the missile for tracking message queue size). In short, this means that the further the missile is from the transceiver, the harder it is to send timely commands to it.
Now, I know that balance changes like this need serious discussion, and I look forward to hearing reasoned, constructive feedback. At the moment, the formula determining delay is (distance/110)^3.